Давайте сперва разберёмся, что такое энтропия, как применить это понятие к нашему вопросу и почему она возрастает.

Энтропия – мера возможностей

Все знают магические слова: «энтропия – мера беспорядка», но мало кто задумывается о том, что за беспорядок имеется в виду.

Строго говоря (по определению), энтропия данного макросостояния системы – величина, пропорциональная логарифму числа микросостояний, которыми реализуется данное макросостояние. Понятнее не стало? Давайте разбираться.

Простой пример: у нас есть два спичечных коробка и четыре спички. С нашей макроскопической точки зрения спички неразличимы, одна ничем не хуже другой. Для нас важно только, сколько в каком коробке находится спичек. Это макроописание системы. Однако, на микроуровне (на уровне спичек) они (спички) различимы и их можно, например, пронумеровать и раскладывать в коробки разными способами, получая одну и ту же макроконфигурацию. Сколькими способами мы можем реализовать макросостояние: в первой коробке – одна спичка, во второй – три (обозначим это состояние 1 + 3)? Или иначе, сколькими способами мы можем разложить четыре неодинаковые спички по двум коробкам, получая заданное макросостояние 1 + 3? Очевидно, таких способов четыре (см. рисунок). А сколькими способами можно реализовать состояние 2 + 2? Шестью (тот же рисунок). Энтропия последнего состояния больше. Энтропия же состояния 0 + 4 равна нулю, так как это состояние реализуется только одним способом (логарифм единицы – ноль).

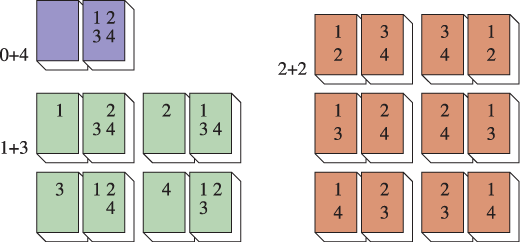
В этом смысле действительно уместна аналогия с порядком и беспорядком. Если все спички лежат в одном месте, это полный порядок и нулевая энтропия. Если всё разбросано хаотично, в беспорядке, то энтропия максимальна. Но это только одна из точек зрения на смысл энтропии.

Я хочу подвести читателя к мысли, что энтропия показывает не столько беспорядок в бытовом смысле этого слова[2], сколько число возможностей для реализации заданного макроскопического состояния (как это и говорилось в определении).

Если рассмотреть больше коробков, то драматизм ситуации ещё более возрастает. Например, для четырёх коробков и восьми спичек конфигурация 1 + 1 + 1 + 5 реализуется 336 способами, а ситуация 2 + 2 + 2 + 2 может реализоваться 2520 способами. Энтропия последнего состояния, как вы понимаете, гораздо больше. Даже минимальное отклонение от этого состояния в состояние типа 2 + 2 + 3 + 1 уменьшит количество возможных реализаций на треть (до значения 1680 шт.).